LUTs (What is a LUT?)

Within the industry there is a lot of confusion regarding working with LUTs, with a lot of people treating LUTs as if they are some form of 'Black Magic'... which they most definitely are not.

So, in an attempt to help explain what LUTs are, and how they work, these pages describe as much about LUTs, and their use, as possible.

But if you just want to get on with building LUTs go directly to the LightSpace CMS page.

LUTs are basically conversion matrices, of different complexities, with the two main options being 1D LUTs or 3D LUTs.

1D LUTs
As an example the start of a 1D LUT could look something like this:
Note: strictly speaking this is 3x 1D LUTs, as each colour (R,G,B) is a 1D LUT

R, G, B
3, 0, 0
5, 2, 1
7, 5, 3
9, 9, 9

Which means that:
For an input value of 0 for R, G, and B, the output is R=3, G=0, B=0
For an input value of 1 for R, G, and B, the output is R=5, G=2, B=1
For an input value of 2 for R, G, and B, the output is R=7, G=5, B=3
For an input value of 3 for R, G, and B, the output is R=9, G=9, B=9

Which is a weird LUT, but you see that for a given value of R, G, or B input, there is a given value of R, G, and B output.

So, if a pixel had an input value of 3, 1, 0 for RGB, the output pixel would be 9, 2, 0.

If the R input value changes to 2, but G and B stay the same, only the R output value changes, with the output pixel values being 7, 2, 0.

Make sense?

This can be shown graphically, like this:

It's easy to see that changing the input value of any one colour only affects that colour's output value. The RGB data is 'decoupled'.

3D LUTs
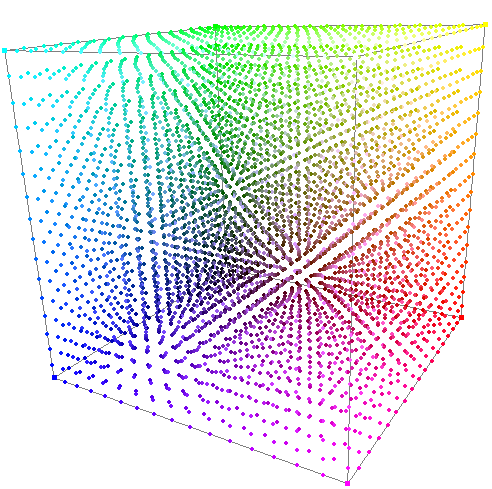
3D LUTs are a little bit more complex, and are based on a three-dimensional Cube with the ability to alter a given single R, G, or B output value based on a single R, G or B input value change.

This is probably best shown graphically, like this:

Looking at the point where all three colour planes intersect (the LUT output point for the given input values) it can be seen that changing any one input colour will cause a change in all three output colour values... a change in any one colour can cause a cross colour change in the other colours.

Hopefully, you can see that as the colour 'planes' move away from the origin point (0, 0, 0) in the direction of their individual axis they will increase in their respective colour, as indicated.

1D vs. 3D
So, 3D LUT are way better than 1D then?

Looking at the 1D vs. 3D comparison at the bottom of this page you'd think so, wouldn't you?

Well, this depends on the LUT requirement and application...

A 1D LUT tends to have values for each and every input to output value, so they are very accurate within their 1D conversions.

If a 3D LUT were to have values for each and every input to output combination the LUT would be very, very large indeed - so large as to be impossible to use. A 3D LUT using every input to output value for 10 bit image workflows would be a 1024 point LUT, and would have 1,073,741,824 points.

So, most 3D LUTs use 17 point cubes, which means there are 17 input to output points for each axis, and the values in between these points have to be interpolated, and different systems do this do different levels of accuracy, so the exact same 3D LUT used in two different system will, in all probability, produce a subtly different result.

It is very rare to get two systems working with the same 3D LUT to show the exact same result!

The way 3D LUTs are written can also be rather confusing.

There are still usually three columns of numbers, R, G, and B, but usually with Blue changing fastest, then green, then red.

The following is the first few lines from a 'default bypass' 3D LUT - output is equal to input:

R, G, B
0, 0, 0
0, 0, 64
0, 0, 128
0, 0, 192
0, 0, 256
0, 0, 320
0, 0, 384
0, 0, 448
0, 0, 512
0, 0, 576
0, 0, 640
0, 0, 704
0, 0, 768
0, 0, 832
0, 0, 896
0, 0, 960
0, 0, 1023
0, 64, 0
0, 64, 64
0, 64, 128
0, 64, 192
0, 64, 256
0, 64, 320
0, 64, 384
0, 64, 448
0, 64, 512
0, 64, 576
0, 64, 640
0, 64, 704
0, 64, 768
0, 64, 832
0, 64, 896
0, 64, 960
0, 64, 1023
0, 128, 0
0, 128, 64
0, 128, 128
0, 128, 192
0, 128, 256
0, 128, 320
0, 128, 384
..., ..., ...

What can be seen is that Blue goes through its 17 point cycle, quickly, Green is updating its cycle once for 17 of Blue's cycles, and Red will update once during the whole length of the LUT, which is equal to Green going through 17 cycles.

These 42 lines continue for a total of 4913 lines...

Easy!

Ok, not so easy... Think of it this way:

In the above 'cube' diagram the Red plane starts in the first of its 17 points (positions).
The Green plane is also at its first point, as is Blue.
The output value for this position is recorded as the fist line of the LUT (0, 0, 0).
The Red plane stays where it is, as does the Green, and Blue moves to its second position.
The output value for this position is recorded as the second line of the LUT (0, 0, 64).
This continues for all 17 points (positions) for Blue.
Then Green is moved to its second point, and Blue goes through its 17 points again.
When Green has been through all 17 of its points, Red is moved to its second point, and the cycle begins again...

Make sense now?

So, for a LUT that isn't a bypass LUT, the position of each 'plane' is altered for each of the 17 points to generate the desired output value.

The first few lines from a real 'calibration 3D LUT' would therefore be something like:

R, G, B
0, 0, 0
0, 0, 36
0, 0, 112
0, 0, 188
0, 0, 261
0, 0, 341
0, 0, 425
0, 0, 509
0, 0, 594
0, 0, 682
0, 0, 771
0, 0, 859
0, 0, 955
0, 0, 1023
0, 0, 1023
0, 0, 1023
0, 0, 1023
0, 32, 0
0, 28, 28
0, 28, 96
0, 24, 172
0, 24, 252
0, 20, 333
0, 20, 417
0, 12, 501
0, 12, 586
0, 8, 674
0, 4, 762
0, 4, 851
0, 0, 943
0, 0, 1023
0, 0, 1023
0, 0, 1023
0, 0, 1023
0, 92, 0
0, 88, 20
0, 88, 88
0, 88, 164
0, 84, 244
0, 84, 321
0, 80, 405
..., ..., ...

What A LUT Does
So, in essence, what a LUT does is take an input value and generate a new output value.

In general (and totally ignoring what has been said above about the accuracy of 3D LUTs vs, 1D), 1D LUTs have their uses, but 3D LUTs can be a lot more accurate, specifically as they can alter saturation (gamut) and cross colour elements (a 1D LUT cannot show a black & white image from a colour one for example), and a 1D LUT is capable of only altering a single output colour value based on a single input value, so has no cross colour component, which can be critical in accurate calibration... In the real world a change in Red value will often cause a (smaller) change in Green and Blue, etc...

The following Marcy image shows the difference between a 1D LUT and a 3D Cube.

The initial image is a 1D LUT and when you hover your mouse over it the image will show the result of a 3D Cube, both LUTs being based on exactly the same data.

As can be seen the major differences are in the levels of saturation as a 1D LUT cannot alter saturation separately to brightness.

This doesn't mean 1D LUTs are of no use, as they can be used to great effect a lot of the time where 3D LUTs are really overkill. On-set viewing where the actual viewing conditions are not good is a perfect application for example, especially as the various cameras that shoot in an 'extended range' mode only adjust their effective gamma, so a 1D LUT can be perfect in displaying a 'viewing' image.

LUT Sizes
There is a lot of confusion regarding LUT sizes, and what the reality as to what is a good size, or not.

There are three main parts to LUT sizes...
First, the actual size of a given LUT that is to be used is primarily defined by the size any given DI system or LUT Box can use. Sizes from 17 to 64 point are common.

The LUT size any given system is designed to used is based on being real-time, so as a rule of thumb higher-end system are able to utilise large LUT sizes. So, saying LUT size is an issue is factually wrong - it depends on the DI system (or LUT box) as to the size it can and will use.

The second, and potentially more important, part to LUT size is building the LUT from profile data, when using LUTs to calibrate displays.

Generating the LUT profile data is what takes time, as a very accurate profile of any given display will be required to generate an accurate result. The same is true when generating profile data for a film lab profile, where film negative and film print stocks need to be accurately profiled using density measurements.

Technical LUTs (not calibration LUTs) are easy to generate as there is no need to profile a display. So, any size is easy - it's just a formula to generate the resultant LUT.

This is also true of 'creative LUTs' as the approach is to make a grade and then RIP the LUT from the grade, at what ever size is required.

When making calibration LUTs you HAVE to profile as many points as possible (regardless of some calibration systems attempting avoid this by using 'guess-work' based profiling, using less points). So, the problem is the time it takes to make the profile, and anything above 17 is just not viable in reality.

The third point is how you then generate a bigger LUT from the smaller profile... You need some very good internal colour engine processing to do this during the LUT generation, and this is where LightSpace is very good.

Some DI systems and LUT boxes also use good LUT interpolation internally, so can use a 17 point LUT and get very good results. Others don't! These bad interpolation systems need bigger LUTs as they can't do the interpolation themselves.